В геометрии существует важное свойство, касающееся суммы противоположных углов четырехугольника. Данная статья раскрывает это свойство и условия, при которых оно выполняется.
Содержание
В геометрии существует важное свойство, касающееся суммы противоположных углов четырехугольника. Данная статья раскрывает это свойство и условия, при которых оно выполняется.
Основная теорема
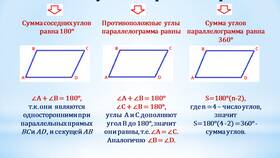
Для вписанного четырехугольника (четырехугольника, который можно вписать в окружность) сумма каждой пары противоположных углов равна 180 градусам:
| Угол A | Угол C | Сумма |
| α | γ | 180° |
| Угол B | Угол D | Сумма |
| β | δ | 180° |
Доказательство свойства
Для вписанного четырехугольника ABCD:
- Центральный угол, опирающийся на дугу ADC, равен 2∠B
- Центральный угол, опирающийся на дугу ABC, равен 2∠D
- Сумма этих центральных углов составляет 360°
- Следовательно: 2∠B + 2∠D = 360° ⇒ ∠B + ∠D = 180°
Примеры четырехугольников
Свойство выполняется для следующих видов четырехугольников:
- Прямоугольник
- Равнобедренная трапеция
- Любой вписанный четырехугольник
- Квадрат
Исключения
Для произвольного четырехугольника, не вписанного в окружность, сумма противоположных углов не равна 180°.
Практическое применение
| Область применения | Использование свойства |
| Геодезия | Проверка точности измерений |
| Архитектура | Проектирование арок и сводов |
| Механика | Расчет четырехзвенных механизмов |
Заключение
Сумма противоположных углов четырехугольника равна 180 градусам только в случае, когда четырехугольник можно вписать в окружность. Это свойство является важным критерием для определения типа четырехугольника и находит практическое применение в различных областях науки и техники.
